一、随机森林算法简介

随机森林属于集成学习（Ensemble Learning）中的bagging算法。Bagging (bootstrap aggregating)

Bagging即套袋法，其算法过程如下：

A）从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本（有放回的抽样）。共进行k轮抽取，得到k个训练集。（k个训练集之间是相互独立的）

B）每次使用一个训练集得到一个模型，k个训练集共得到k个模型。

C）对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。

 

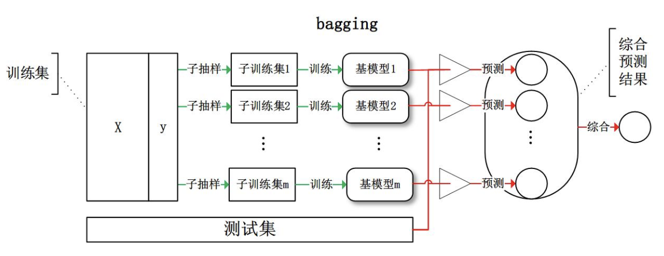
Random forest(RF)=bagging + fully-grown CART decision tree

Random Forest的random体现在bagging，Forest是因为采用的CART树模型作为基学习器。决策树训练速度很快，但容易过拟合，即有很高的variance，而bagging采取多个模型投票或者平均，可以降低variance，随机森林的方法就是用bagging的方法把decesion tree合起来。

随机森立中的每棵树的按照如下规则生成：

　　1）如果训练集大小为N，对于每棵树而言，随机且有放回地从训练集中的抽取N个训练样本（这种采样方式称为bootstrap sample方法），作为该树的训练集；

　　2）如果每个样本的特征维度为M，指定一个常数m<<M，随机地从M个特征中选取m个特征子集，每次树进行分裂时，从这m个特征中选择最优的；

　　3）每棵树都尽最大程度的生长，并且没有剪枝过程。

一开始我们提到的随机森林中的“随机”就是指的这里的两个随机性。两个随机性的引入对随机森林的分类性能至关重要。由于它们的引入，使得随机森林不容易陷入过拟合，并且具有很好得抗噪能力（比如：对缺省值不敏感）。

按这种算法得到的随机森林中的每一棵都是很弱的，但是大家组合起来就很厉害了。可以这样比喻随机森林算法：每一棵决策树就是一个精通于某一个窄领域的专家（因为我们从M个feature中选择m让每一棵决策树进行学习），这样在随机森林中就有了很多个精通不同领域的专家，对一个新的问题（新的输入数据），可以用不同的角度去看待它，最终由各个专家，投票得到结果。

随机森林的特色体现在OOB估计以及特征选择上，接下来介绍RF的这两个重要特性

二、OOB(out of bag)估计

我们知道，在构建每棵树时，我们对训练集使用了不同的bootstrap sample（随机且有放回地抽取）。所以对于每棵树而言（假设对于第k棵树），大约有1/3的训练实例没有参与第k棵树的生成，它们称为第k棵树的oob样本。

为什么是1/3呢，证明如下：

 

但我们不需要用OOB样本来验证每个基学习器，用OOB样本来验证bagging后的模型才更有意义。

oob Estimate的过程如下：

　　1）对每个样本，计算它作为oob样本的树对它的分类情况（约1/3的树）；

　　2）然后以简单多数投票作为该样本的分类结果；

　　3）最后用误分个数占样本总数的比率（或者是误差函数的值）作为随机森林的oob误分率。

由于采用了oob估计，RF不需要像传统的机器学习算法用计算量庞大的交叉验证来模型的准确率，而且需要划分训练集和验证集，只能用小部分的样本集来训练模型， RF可以用所有样本集来训练。

RF有一个重要的优点就是，没有必要对它进行交叉验证或者用一个独立的测试集来获得误差的一个无偏估计。它可以在内部进行评估，也就是说在生成的过程中就可以对误差建立一个无偏估计。

 

三、特征选择 

线性模型中的特征选择：每个特征的样本值做归一化后，就可以用系数的绝对值大小来判别特征的重要性，但是无法对线性不可分的样本集做特征选择。

 

随机森林中的特征选择:

基本想法：如果特征i对模型是有利的，那么将第i维特征置换为随机值，将会降低模型的性能。将某个特征的值重新随机排列，这样的好处是不改变原始数据的分布。

将完整模型的性能减去置换第i维特征后的模型，就得到了第i维特征的重要性。

要评估置换第i维特征后的模型性能，正常想法是要重新训练并用验证集来评估性能，但是随机森林中我们可以用OOB error来衡量模型性能，此处同样可以引入OOB error。即在oob验证的时候替换样本的值,从此时的gt的oob样本中随机选取一个样本的特征i的值作为该样本的特征i的值

 

 

参考链接：

台大林轩田老师的《机器学习技法》

https://www.cnblogs.com/maybe2030/p/4585705.html

http://blog.csdn.net/flowerboya/article/details/50916653